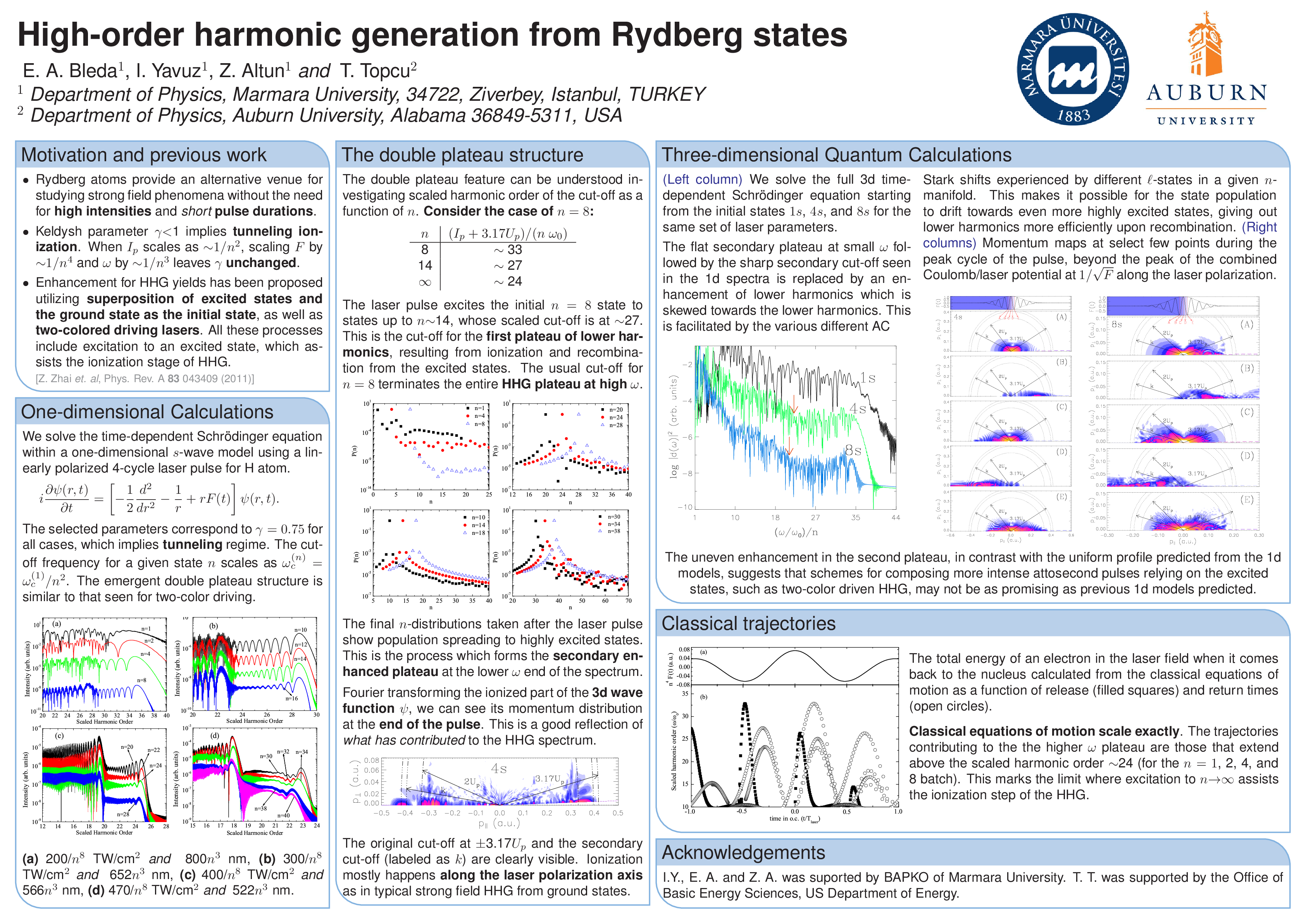
High-harmonic generation from endofullerenes
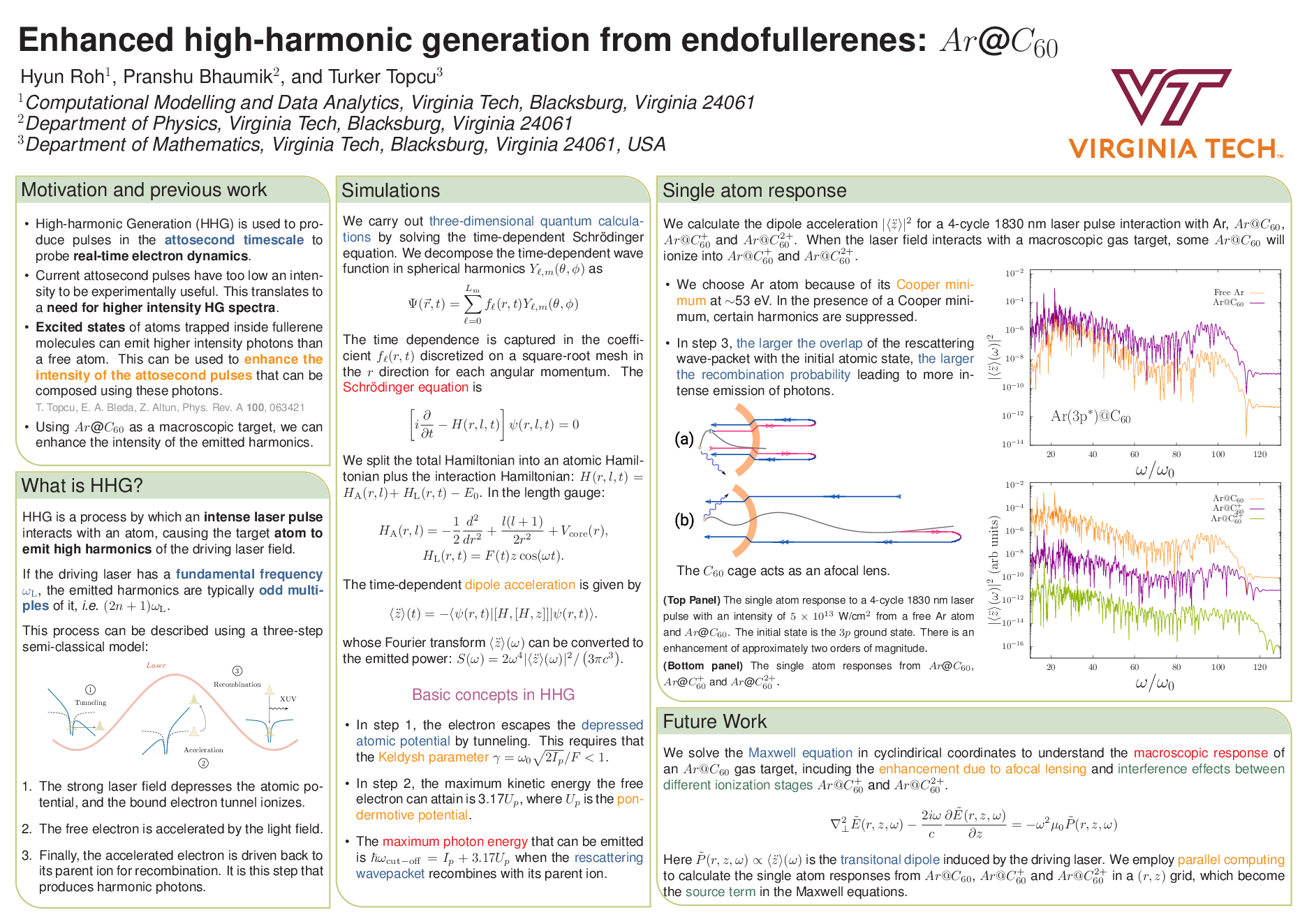
Quasistable Rydberg states in a strong microwave field
An experiment from Tom Gallagher’s group at UVA observed a large fraction of Rydberg atoms excited in the presence of a strong microwave (MW) field survive the strong field. Furthermore, the survival probability showed peaks separated by the MW frequency. This is interesting because weakly bound states are created in strong external fields, and they survive for long times.
To investigate, we solve the time-dependent Schrodinger equation using a Green’s function method in one-dimension for wave packets launched in a 38 THz microwave field. We have also performed full 3d calculations and found that a one-dimensional model can capture the physics involved. Furthermore, we scaled experimental energies down by a factor of 1000, which corresponds to scaling n down by a factor of 10. This reduces the computational overhead substantially because it allows smaller box sizes (smaller n).
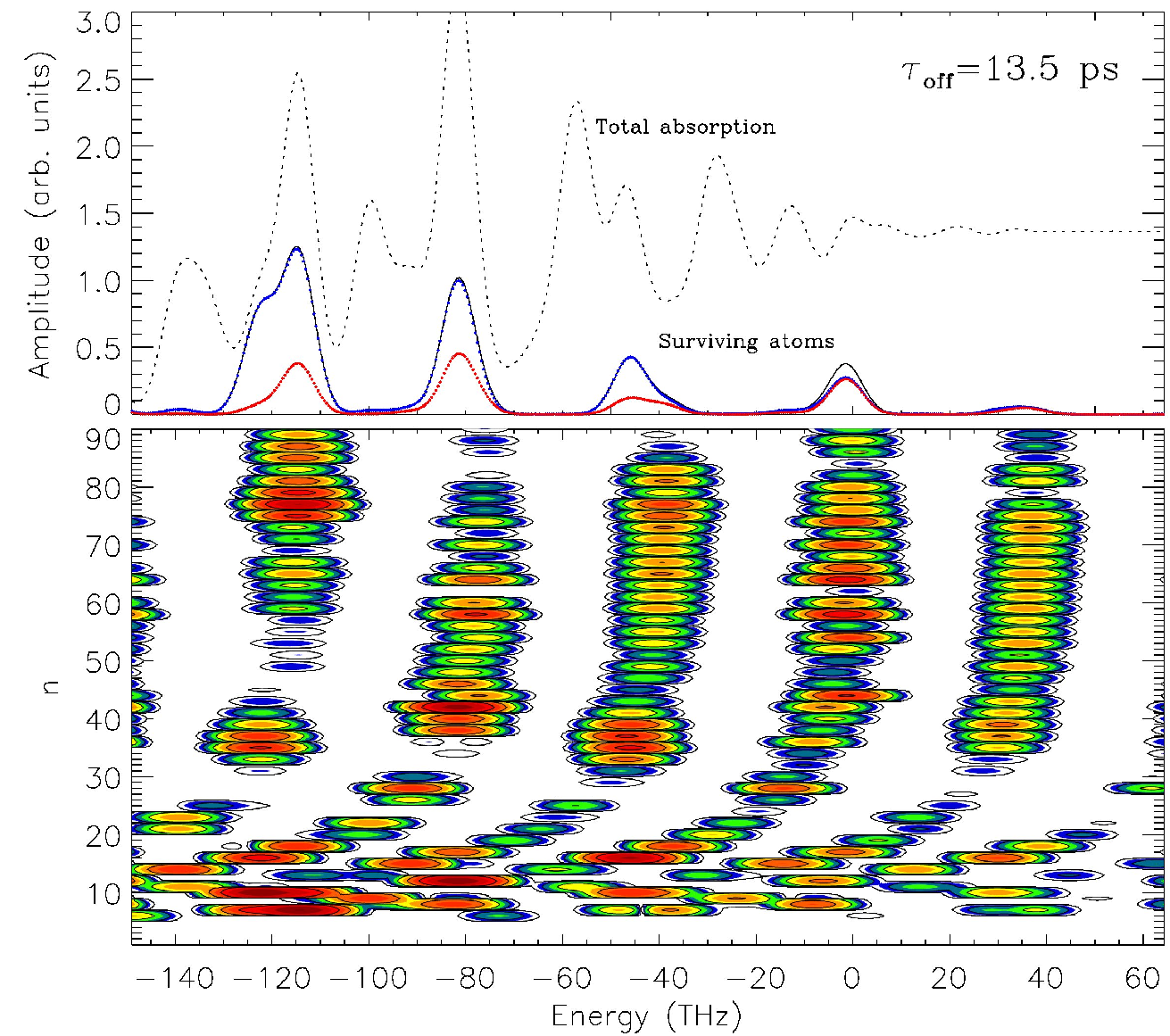The figure [left] shows the surviving population and its binding energy distribution (lower panel) as a function of the excitation energy 13 ps after the peak of the excitation laser. As in the experiment, we find that a substantial fraction of the atoms survive long exposure to a strong microwave field. The survival probability displays peaks at the microwave frequency. The experimental spectra and quantum-mechanical calculations imply that the atoms survive in quasi-stable states. The Rydberg electron is infrequently returning to the ionic core during the field in a weakly bound orbit.
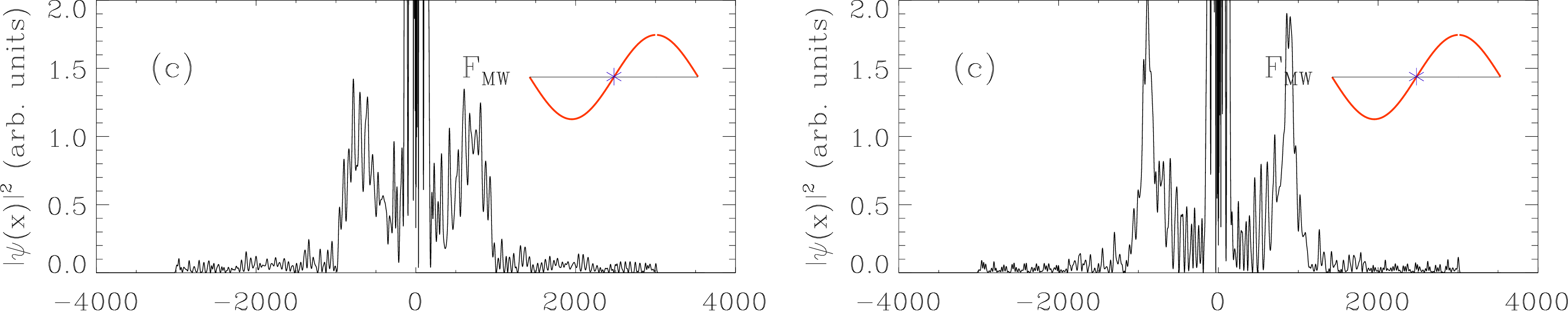
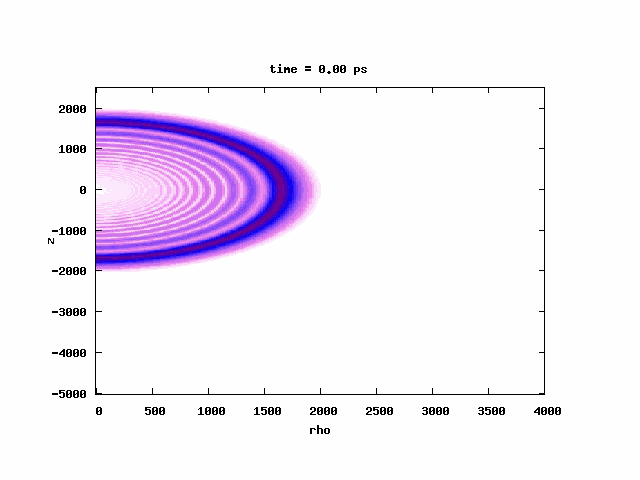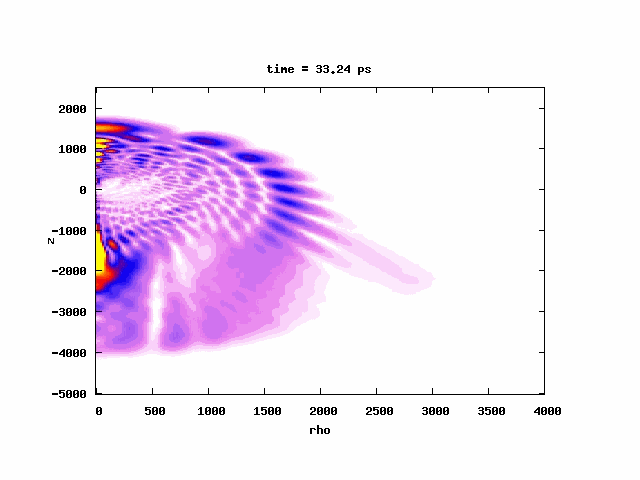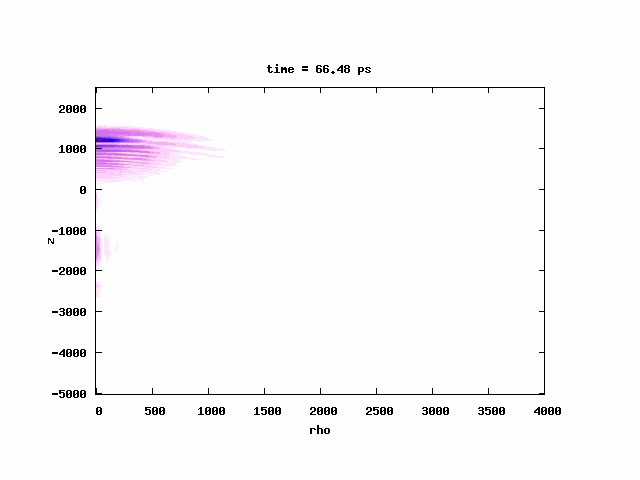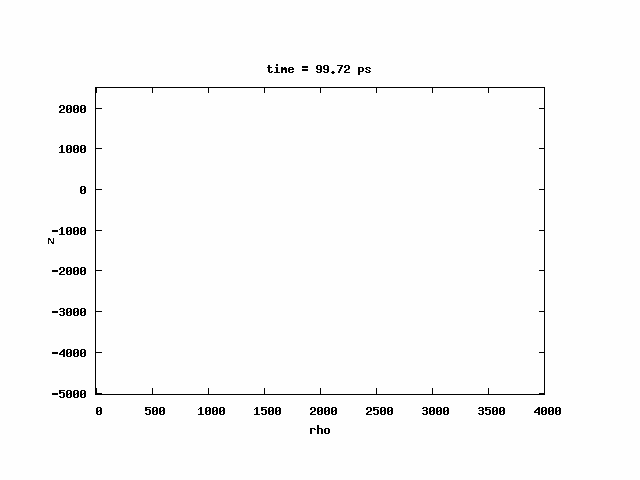
[Below] Probability densities at 153 (left) and 256 (right) microwave cycles from the peak of the excitation laser. In both cases, there is substantial population at n = 21 at |x| = 800 a.u. (the two peaks on either side of the origin). When the atoms are exposed to microwaves for longer times, the peak at the center (low-n population) diminishes much faster than the peaks centered at |x| = 800 a.u. The n = 21 state is within one microwave photon from the threshold and accounts for the population surviving the microwave field for long times. See our paper on this work here.
Keldysh parameter (γ) vesus scaled frequency (Ω) in photoionization
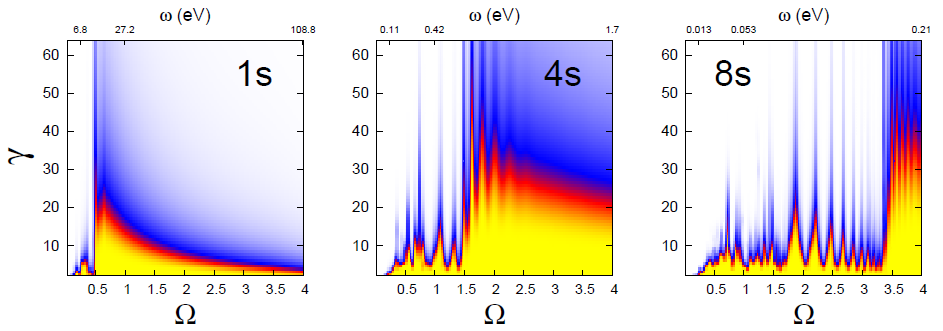
The Keldysh parameter (γ) is commonly used in the intense laser physics community as the parameter which identifies the dominant dynamical ionization regime, whether it be tunneling (γ<1) or multiphoton ionization (γ>1) regime. However, it has also been demonstrated that the Keldysh parameter alone is not suitable for determining the dominant ionization path when a wide range of laser frequencies is considered (See H. R. Reiss, PRL v.82, 023418 (2010)). 
The Keldysh parameter is given by γ = ω √2Ip / F, which can be varied from γ<1 to γ>1 by either varying F while keeping ω constant, or by varying ω while keeping F constant. Therefore situations in which γ<1 do not necessarily point to ionization dynamics dominated by tunnel ionization. We performed fully 3-d quantum simulations to map (γ,Ω) space for ionization rates and ionization probabilities (below) in H for a few low lying excited states. The most prominent features in these maps is the direct/indirect multiphoton ionization peaks that occur before the single-photon ionization limit is reached, after which ionization can be accurately described by the time-dependent perturbation theory (Fermi’s golden rule).
Furthermore, we calculate the momentum distributions of the ionized electrons for various (γ,Ω) pairs for the 1s and the 4s initials states (left) for a fixed Keldysh parameter γ=4. Although these should result in tunnel ionization in the Keldysh picture, we have found a transitory region in Ω, which separates the tunneling and multiphoton regimes at the same γ<1. For the 1s initial state, the transition occurs around γ~0.25, whereas for the 4s state, the multiphoton absorption rings start to appear in the momentum maps around γ~1.
[Below] Ionization probability out of 1s, 4s and 8s states of the hydrogen atom with a laser pulse of 160 Rydberg periods at FWHM as a function of scaled frequency (Ω) and the Keldysh parameter (γ). The yellow region is where the ionization saturates. Direct and indirect multiphoton ionization regions are marked with the resonance structures before the single-photon ionization limit is reached. The simulations were carried out at NERSC center with 12,000 points for each (γ,Ω) map.
See our published work for a detailed account here.
See the DAMOP 2012 poster here.
Selective Field Ionization in Strong Magnetic Fields with Rydberg Atoms
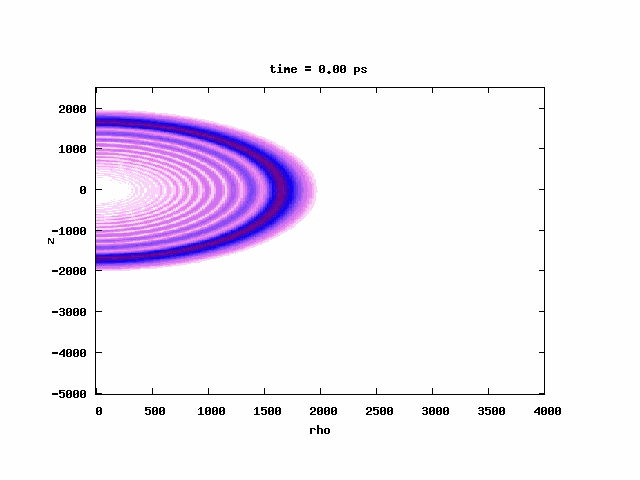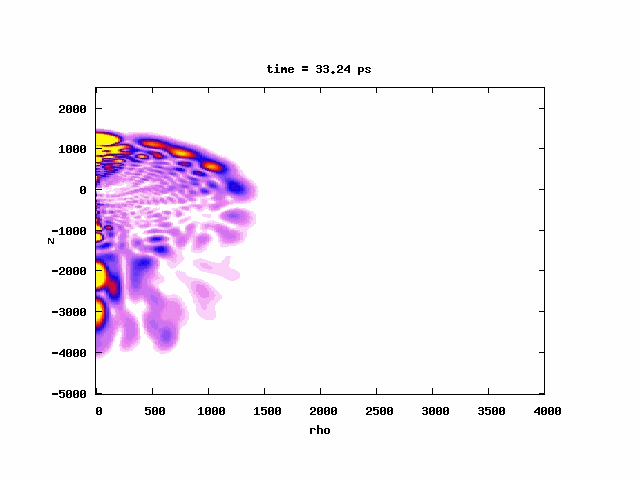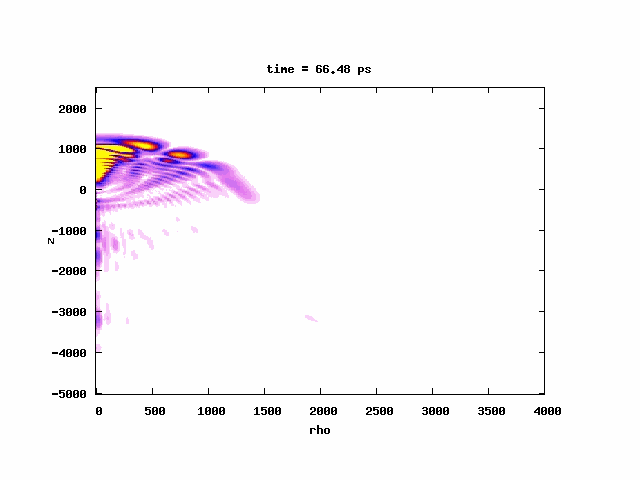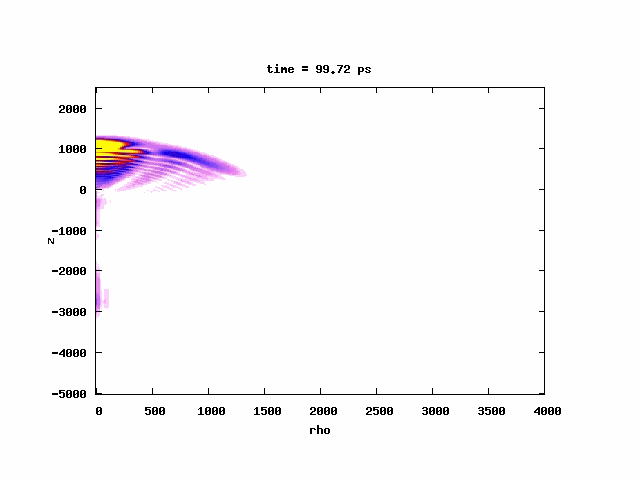A problem initially inspired by the experiments from Michigan group (Phys. Rev. Lett. 95, 253005 (2005)) in which they excited atoms to a very high-n band near/above threshold in strong uniform magnetic field. Linearly ramping up an external E-field (SFI), they observed Landau quantization of the energy levels and spin-flips. The magnetic fields in their experiments (6T and 2.9T) were so large for the excited energy bands they had (168GHz and 81GHz wide bands above threshold) such that the electron was essentially bound by the uniform magnetic field through its spin. The time scales involved are in μs. Published in Journal of Physics B: J. Phys. B 44, 184003 (2011) or Local linkHigh-order harmonic generation in the presence of noise
We performed numerical simulations of HHG by solving the stochastic time-dependent Schrodinger equation to observe effects of stochastic enhancement predicted by Singh et al. (PRA v.76 063403 (2007)) for ionization on the high harmonic spectra when an atom is driven with an IR pulse superposed with white noise. A large net enhancement in the total ionization yield would not necessarily translate into a net enhancement in the HHG yield since the harmonic generation process involves ionization followed by recombination. The amount of increase a stochastic resonance can induce in the HHG yield would depend on what fraction of the ionized electrons (e.g., in the first step of the three-step model) have low enough kinetic energy when they end up in the continuum so that they can be recombined with the parent ion. Our calculations show that when an optimum amount of noise is present in the driving laser field, roughly a factor of 45 net enhancement can be achieved in high-order harmonic yield.
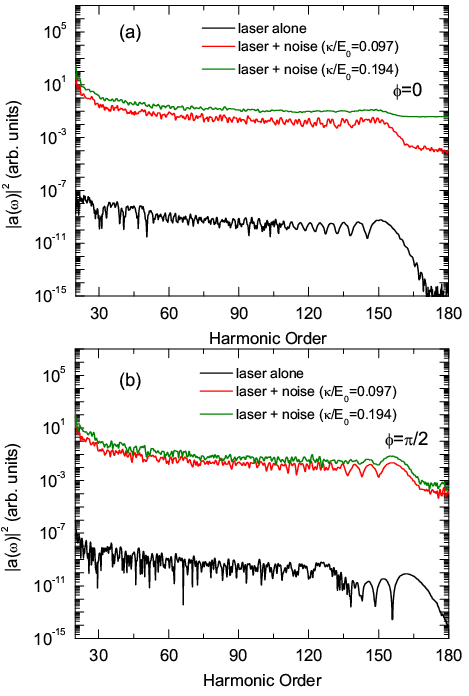
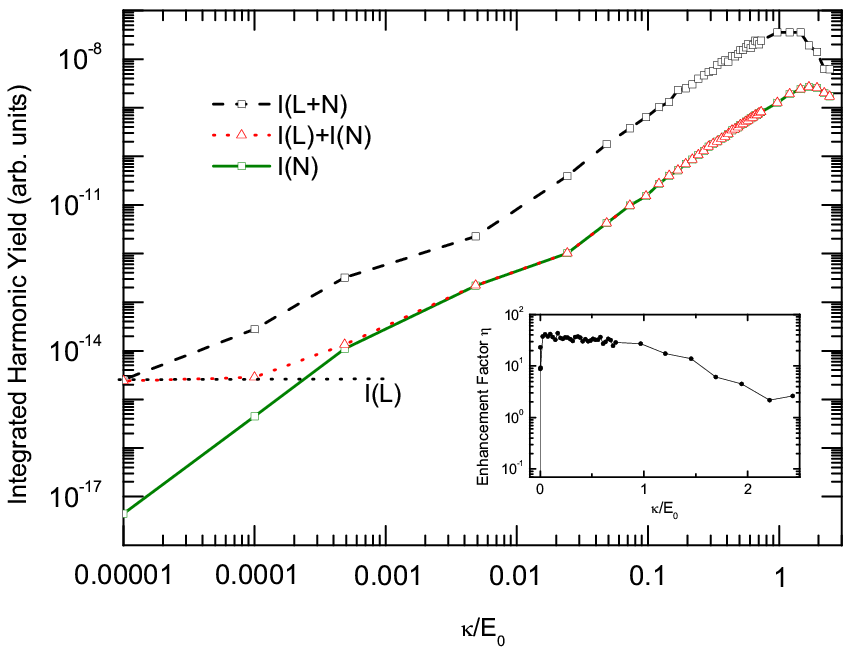
The figures above are for He+ with a 10.8 fs laser pulse of 800 nm wavelength. The relevant quantity we investigated is the ratio of the noise amplitude to the peak laser field strength. Single-atom HHG spectra from both noisy and noise-free drivings are shown in the figures above for comparison.
Published in Journal of Physics B: J. Phys. B 44, 135403 (2011) or Local link
A Tentative List of Future Projects
- Dramatic Enhancement of HHG in mixed gas samples (Xe and He). The HHG yield from the species with lower Ip can drive the other species for HHG along with the fundamental pulse. Can draw analogy to two color driving. See PRL 99, 053904, (2007) by Takahashi et al. for the experiment.
- HHG from confined Rydberg atoms
- Representation problem in solving the electron-Rydberg scattering problem (see this paper by Rabitz et al. on Hamiltonian Encoding.)
- Revisiting ADI methods (e.g. Peaceman-Rachford algorithm) for propagation of the time-dependent Schrodinger equation. Also see The Computer Journal 8 (2), 166, 1965.