Multiphoton adiabatic rapid passage: twist and non-twist conditions
The problems on population transfer via multiphoton adiabatic rapid passage (mARP) we studied so far (microwave driven and kicked Rydberg atoms, IR driven molecule) had the property that the classical frequency of the system increased with energy. However, in a rotor problem, the frequency decreases with energy, but the exact dynamical mechanism still works since the frequency changes monotonically with energy (classical twist condition). An interesting question arises as to what would happen if the frequency first increases and then decreases as a function of energy (the non-twist condition). Quantum mechanically, this corresponds to increasing and then decreasing nearest-neighbor energy spacings in the bound spectrum. This would prevent a ladder-climbing scheme from working the way it did when the frequency changed monotonically. You can see some slides here.
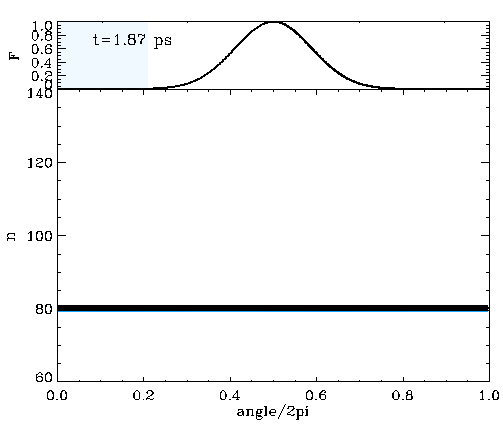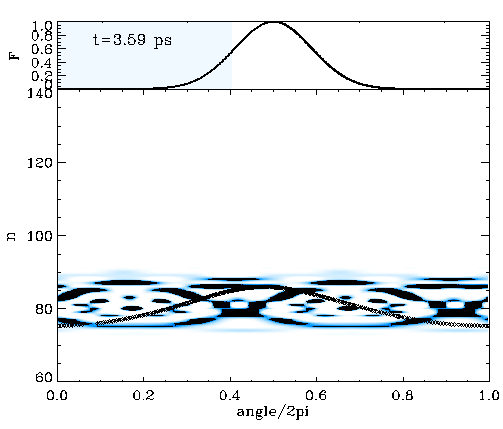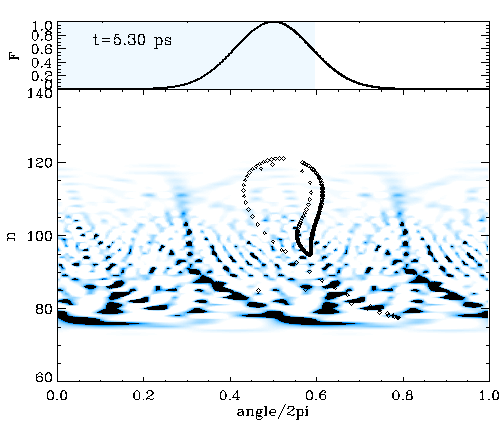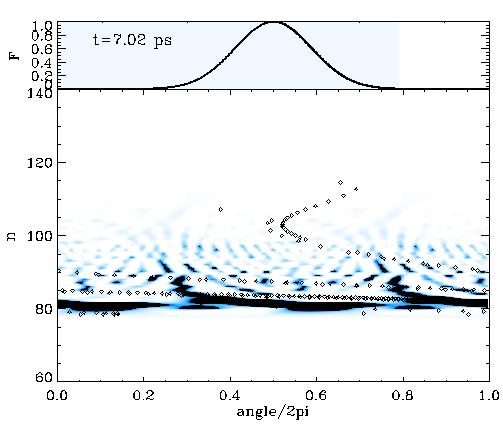
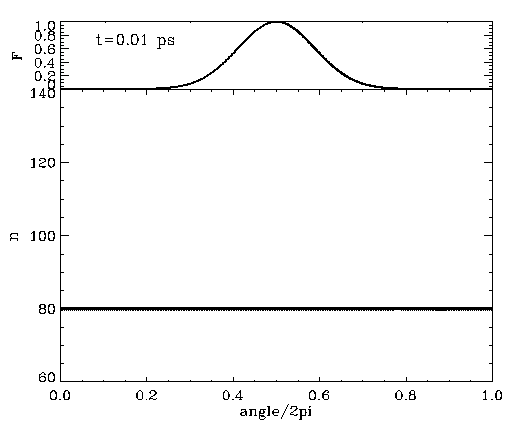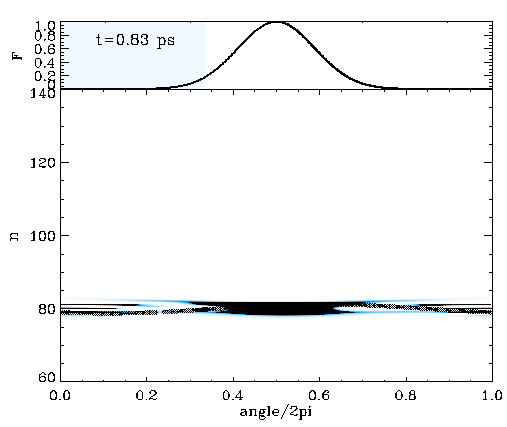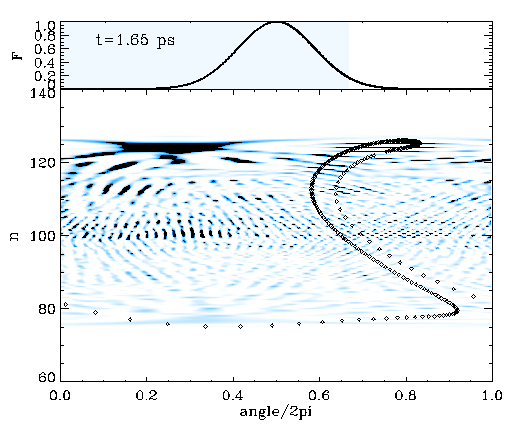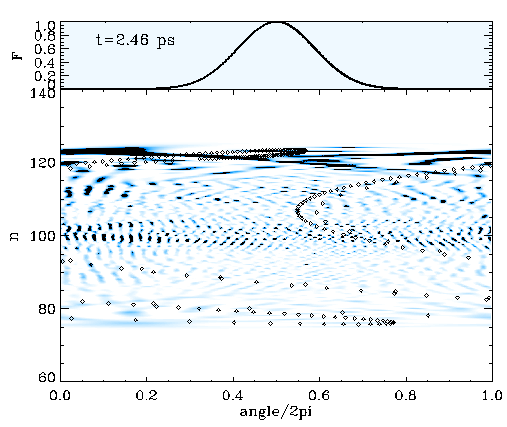
We considered a particle in a box with a relatively flat bottom, U(x)=e-(x/L)4, to simulate such an energy-frequency profile. The movie on the left shows the time evolution of the classical trajectories (dots) in phase space on top of the corresponding quantum mechanical Wigner distribution. The driving pulse is a Gaussian, and its envelope is seen on top of the movie. Both classical and quantum calculations are one-dimensional, and the system initially starts in the n=80 state. The shearless curve is roughly at n=100, and the population is transferred in action by the same amount the initial state was below the shearless curve. The population keeps oscillating between n=80 and n=120, which brings an extra time scale to the problem.
The movie on the left demonstrates that almost the entire population can be transferred to n=120 above the shearless curve by adequately timing the pulse duration. We have found that the underlying classical phase space mechanism works the same irrespective of whether the driving is sinusoidal or consists of a train of impulsive kicks. We have also found that by chirping the driving pulse, it is possible to remove the extra time scale and render the necessity of timing the driving pulse redundant. In the latter case, the wider the driving pulse envelope, the sharper the final n-distribution of the population around n=120.
See our article for a detailed account: Phys. Rev. E 83, 046607 (2011) or Local link.
Population Transfer in a Kicked Rydberg Atom
Following up on the multiphoton population transfer in a microwave-driven atom, we showed that the same physical mechanism could be exploited to drive resonant transitions in a Li atom using a chirped train of impulsive kicks rather than microwaves. The underlying classical process is the same as the one observed for the driven atom, except that, owing to the high-frequency components inherent in the kicks, the classical phase space is sticky. Classically this calls for higher peak field strengths to induce transitions. Final n-distributions are spread out around the final n-manifold due to this necessity for stronger driving. We observed stark differences between kicked and microwave-driven atoms in their l-distributions. In the kicked case, the entire population was confined within l < 5 compared to l ~ (n-1) in the microwave-driven case.
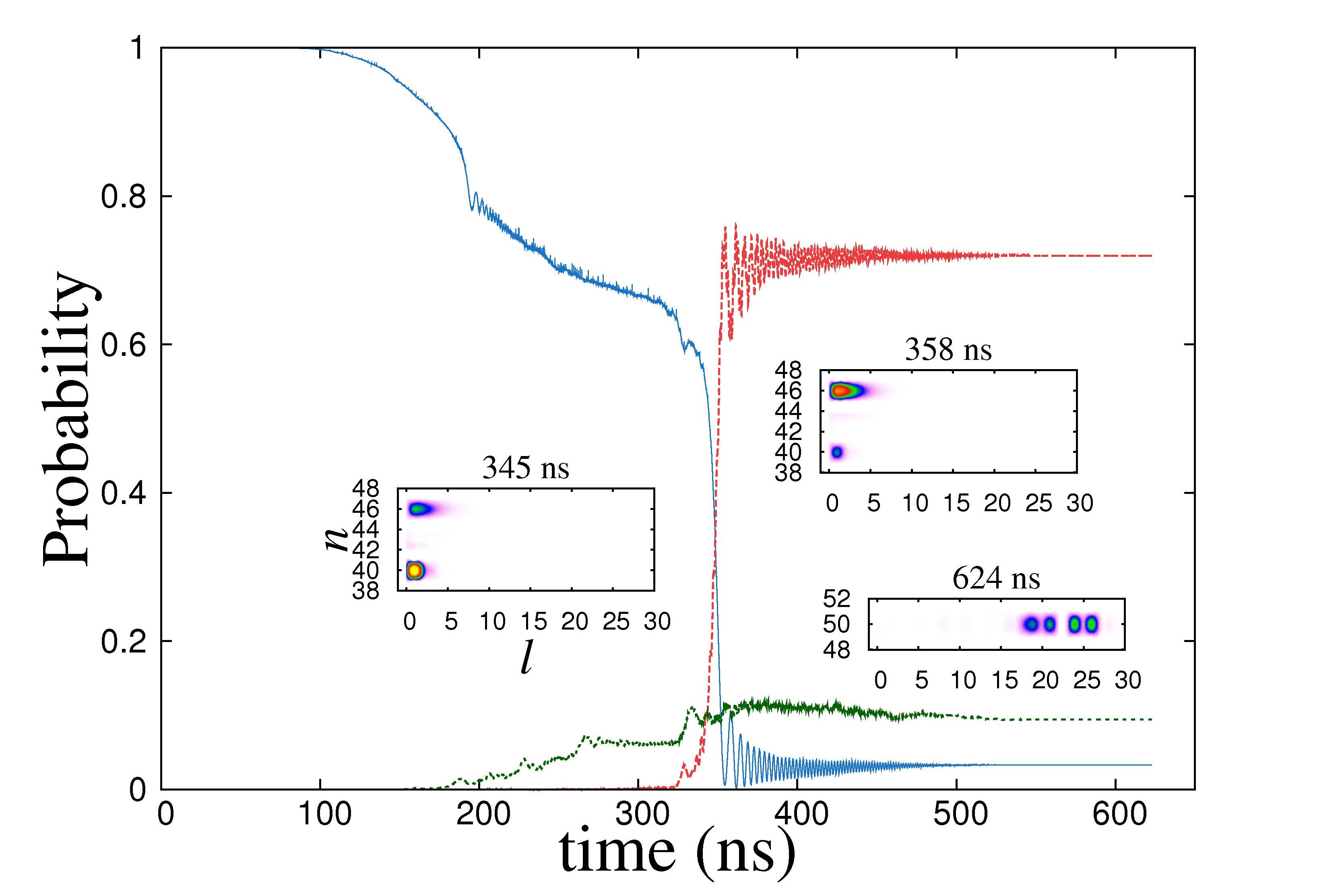Above is the time-dependent probability for kicked Li atom initially in the 40p state (blue curve) when the kick frequency is chirped through a 4-photon resonance condition. After the kick pulse is turned off, roughly 74% of the population ends up in n=46 (red curve) and about 12% in n=50 (green curve). Inserts are the (n,l)-distributions just before (345 ns), after the transition takes place (358 ns), and after the pulse is completely turned off (624 ns). See our article for a detailed account: J. Phys. B 43, 115003 (2010) or Local link.
This work has been highlighted in July-August 2010 issue of Europhysics News. [Local link]
You can also see some slides here.
Population Transfer in IR Driven HF molecule
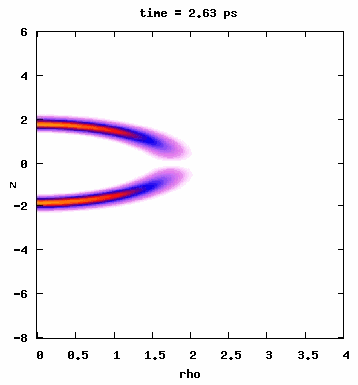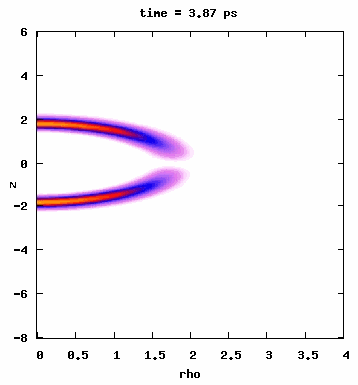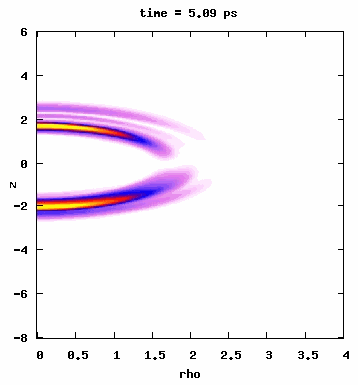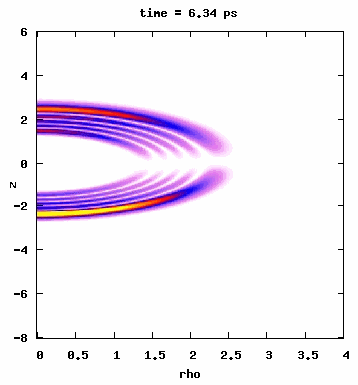
The quantum mechanical process responsible for the efficient multiphoton population transfer in the microwave drivenRydberg atom can be alternatively looked upon as a classical transition in phase space. This classical mechanism is rather generic and can be made to work in many different systems. One example we considered is the driven Morse oscillator, which is commonly used to model vibrational modes of diatomic molecules. The figures below show results from our 3-dimensional quantum simulations where we drove the ground state of HF up to n=4 by chirping an IR pulse through a 4-photon resonance condition. As seen from the top panel (left-hand figure), we observe complete population transfer into the n=4 manifold. The bottom panel shows J distribution as a function of time. The animation on the right-hand side shows the time evolution of the absolute value square of the wave function. You can see some slides here.
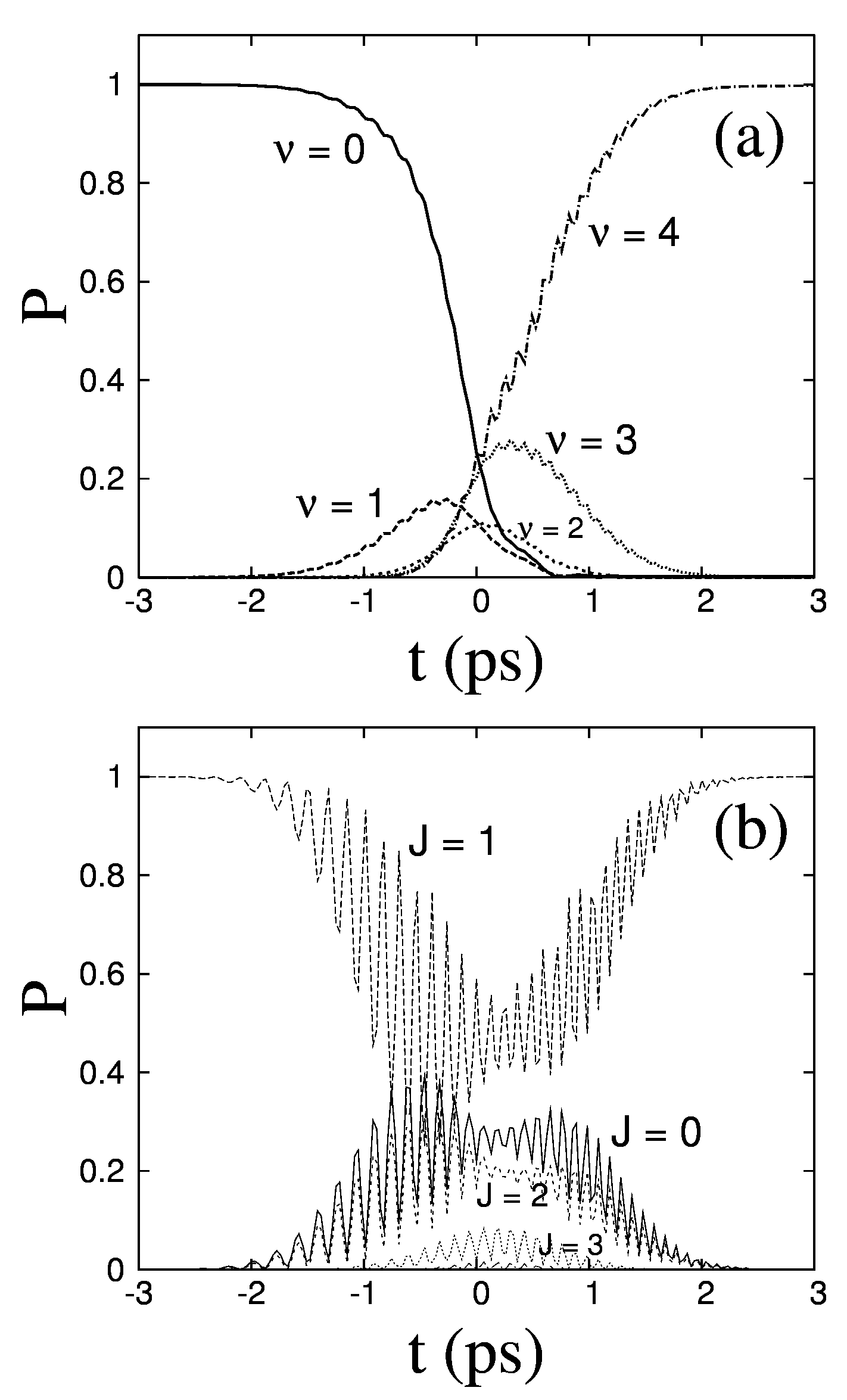This is different from a microwave-driven Rydberg atom because in this case, we start from the ground state. Therefore, initially, there are no states available below the initial state, which can potentially influence the transition since many lower energy states can provide different pathways through virtual transitions. However, starting with the lowest possible classical action (ground state) does not change the dynamics observed in a microwave-driven molecule (right-hand figure). Published in Journal of Physics B: J. Phys. B 43, 115003 (2010) or Local link.
