Computational approach to quantum gate evaluation and design in
neutral atom quantum information processing
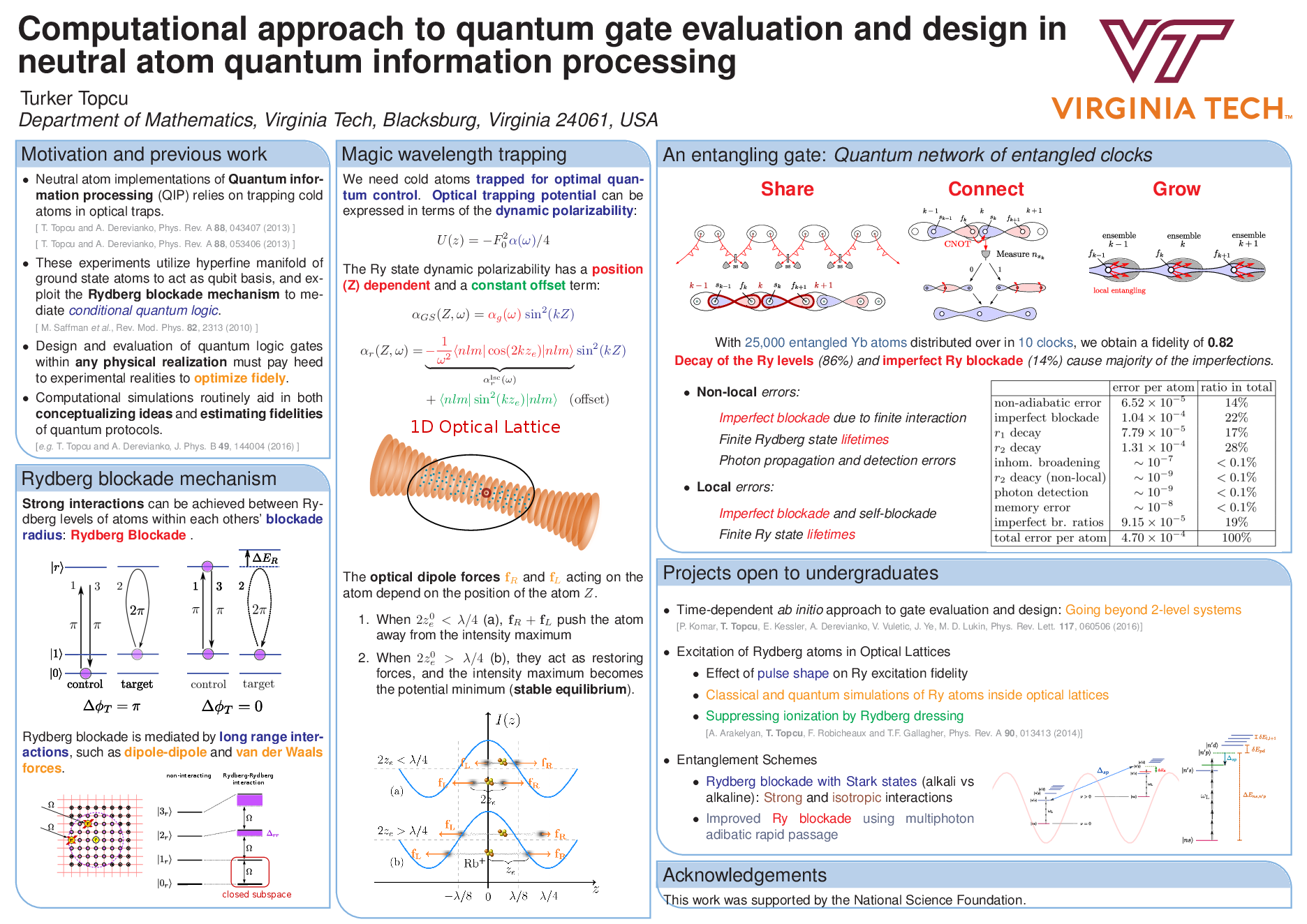
An entangled network of quantum clocks

I collaborated with an experimental group at Harvard for entangling a network of atomic ensembles for realizing a distributed atomic clock near the Heisenberg limit. This distributed architecture can also provide an international time scale (see PRL v.112, 190403 (2014) and Nature Phys. v.10, 582 (2014)). We are ultimately interested in making atomic clocks, and we are particularly interested in using Sr and Yb trapped in an optical lattice. A recent scheme for generating maximally entangled alkali-metal atoms makes use of long-range interactions between Rydberg atoms, particularly Rydberg blockade (Saffman and Molmer, PRL v.102, 240502 (2009)). We have adapted this scheme to be used with Sr and Yb, which involves evaluating long-range interaction strengths between Rydberg atoms and choosing proper states.
Some slides on this work can be seen here. 
State selective trapping of Ry atoms
In general, the tune-out phenomenon for Rydberg states allows one to selectively trap Rydberg atoms in optical lattices depending on the atomic state or the atomic species. The tune-out scheme we proposed above can be used for selectively trapping Rydberg atoms in optical lattices based on their n-state. This is possible chiefly because the trapping potential oscillates with the lattice wavelength changing sign, meaning that at some wavelength, it vanishes. In a lattice where the wavelength is fixed, we can instead vary the principal quantum number n to change the position of the nodes (where the trapping potential is zero) so that it is at the desired lattice wavelength. When this condition is satisfied, the atom becomes unaware of the optical lattice potential.We tabulate optical lattice wavelengths at which select n-states can be tuned out of the lattice and derive an analytic expression capable of predicting half of the available tune-out wavelengths.
See our paper on this work here.
Magic trapping Rydberg atoms in optical lattices
Recent advances in precision timekeeping, quantum control with cold molecules, and quantum computation science heavily rely on trapping cold atoms and molecules in optical lattices. For example, long-range interactions between neutral Rydberg atoms have emerged as a potential means for implementing logical quantum gates to realize scalable quantum computing. These experiments utilize hyperfine manifolds of ground-state atoms to act as a qubit basis while exploiting the Rydberg blockade mechanism to mediate conditional quantum logic. Several decoherence sources must be overcome for such gate operations to have high fidelity. Magic wavelength trapping in optical lattices has emerged as an indispensable tool for gate experiments. It eliminates the differential energy shift between the qubit and the Rydberg state experienced by the atom as it moves inside the optical lattice.
The common wisdom is that alkali metal atoms in Rydberg states see trapping potentials that are essentially that of a free electron, and can only be trapped at laser intensity minima. We have demonstrated that this is not the case from the first principles. We find a non-monotonic interplay between the lattice constant and the physical size of the Rydberg state. We elucidated this interplay using a simple toy model. We showed that the size of the Rydberg orbit relative to the lattice constant determines whether a Rydberg atom is trapped at intensity minima or maxima. Through extensive calculations, we confirm the physics behind this simple toy model for a realistic alkali atom, and discover that the trapping potential seen by the Rydberg electron is composed of an intensity-modulated landscaping term and a constant offset, which does not depend on the position of the atom along the lattice. This opens up an exciting possibility of the magic trapping of alkali atoms in Rydberg states in infrared optical lattices.
Working at these wavelengths in cold atom experiments relying on trapping Rydberg atoms provides several compelling advantages. In quantum gate experiments, the magic trapping scheme we propose renders turning off the trapping fields unnecessary whenever a gate operation is performed. Furthermore, because the wavelengths are near the CO$_2$ laser band, the photon scattering and the ensuing motional heating are reduced compared to conventional traps near low-lying resonances, alleviating another source of decoherence.

